Quantum computing is one of the most exciting emerging technologies, especially with Google’s Sycamore quantum processor demonstrating supremacy in October of 2019. Quantum computing marks a paradigm shift in computing, having the potential to overhaul digital security and fuel scientific breakthroughs. But, what exactly is quantum computing?
Let’s start with classical computing. At the heart of classical computing is the concept of computer logic. Computer logic is comprised of information and information processing. Information is simply strings of 1s and 0s. A conventional computer represents everything — from text to images— as a string of bits (binary digits). All your computer deals with are 1’s and 0’s. Why? Well, these boolean values can be represented by the state of a transistor, which are the building blocks for integrated circuits. In computers, these bits are often represented as a voltage: 0V means 0; 5V means 1. Hence, a wire with current represents a bitstate of 1 and a wire with no current represents a bitstate of 0.
Information processing can be broken down into boolean logic gates. There are 7 primary gates (NOT, AND, OR, NAND, NOR, XOR, XNOR) that take in either 1 or 2 bits as input and output a single bit. Each gate performs a unique operation upon the bit(s), which then determines the output. When these gates are chained together, you get circuits which enable the capabilities of modern computers today.
These gates are comprised of transistors, which in turn are made from semiconductors (like silicon). With transistors, you are able to store any kind of information and process it. A transistor can be thought of as a switch: if it’s ‘on’, electricity is flowing through the wire; if it’s ‘off’, there is no electricity. Modern CPUs have billions of transistors, with the number of transistors roughly doubling every year (this is known as Moore’s Law).
Above is a great video from Intel, showing the process of creating microchips
Despite this massive revolution in computing and information processing, however, there are still problems that are out of reach for even the fastest supercomputers. This is where the necessity for quantum computers comes in.
Quantum computing is not as binary (rather literally) as classical computing. As we’ve seen, classical computers manipulate and process bits, that are represented by voltages; in quantum computing, we use qubits (quantum bits), that are represented by electrons. Quantum computing uses the principles of quantum mechanics to process and manipulate information, namely superposition and entanglement, allowing for some incredible capabilities.
We’ll be looking at these properties from the perspective of quantum computing rather than quantum mechanics. The theory behind quantum mechanics is complex and it’s much easier and relevant to understand their applications in quantum computing.
We think of bits as 1’s and 0’s. Really, bits could be anything with 2 states: true/false; on/off; heads/tails. A classical computer simply quantifies these bits as integers since that’s all a computer can store and process. Qubits, however, are an entirely different beast: they’re vectors. This is because a qubit really represents the probability that its bitstate is either 0 or 1; rather than only being 0 or 1, they can exist as any value between 0 and 1 until they are measured (we’ll touch on this in a bit).
In quantum mechanics, we represent vectors using Dirac notation, which makes quantum computations clearer and more concise. |ψ⟩ denotes a unit column vector and ⟨ψ| denotes a corresponding row vector. ⟨ψ| is the Hermitian transpose of |ψ⟩, which is found be transposing |ψ⟩ and taking the complex conjugate of every entry, represented as ψ†. We represent the classical bits 0 and 1 as column vectors |0⟩ and |1⟩:

Why are qubits vectors? In quantum mechanics, the properties of electrons, more precisely its spin, are unknown until we actually measure its state. Similarly, in quantum computing, the state of a qubit exists as a superposition of all possible states, with an assigned probability of it being 0 or 1; until the qubit is measured (see below), it is both 0 and 1, but with a certain likelihood of collapsing to 0 versus 1. A qubit in a state of superposition is a linear combination of the infinite states that exist between 0 and 1. This can be visualized on a Bloch sphere.
So, when we perform specific operations upon a qubit, we can force it into a superposition, where it is no longer only 0 or only 1; rather, it exists as a certain probability of both. These operations can be thought of as rotating the unit vector around the Bloch sphere in a 3-dimensional real vector space. A vector space is simple the space in which a vector resides in. A simple 2-dimensional vector lies in the vector space ℝ³.
When a qubit is actually measured, it will always be either 0 or 1. The act of measuring the qubit has caused the quantum superposition to collapse, and the qubit’s state is now analogous to classical bits’. Informally, we can consider measuring a qubit as ‘observing’ it. Once a qubit’s superposition has been collapsed, it will remain in that state indefinitely. The value it collapses to depends upon its configuration, which is known as its quantum interference. A qubit can be restored to a superposition state via a quantum gate, which performs an operation upon one or more qubits.
More generally, a qubit’s state can be represented as α|0⟩ + β|1⟩, where α and β are complex numbers (numbers of the form a + bi) denoting the respective probability that the qubit will collapse to either 0 or 1. These coefficients satisfy the equation|α|²+|β|² = 1, as the sum of all probabilities in a system must be 1. So, if the qubit has a 50% chance of collapsing to 0 and a 50% of chance of collapsing to 1, α =1/√2 and β=1/√2.
As seen in the Bloch sphere, |0⟩ and |1⟩ form the basis vectors of the vector space that describes the qubit’s state. α and β can thus be seen as the rotations applied to a vector in a complex vector space. We often arrange α and β in a column vector known as a quantum states vector as shown below:

A single qubit isn’t of much practical use, with a modern calculator subjugating it. The true power Multiple qubits are denoted as a tensor product. If we let α|0⟩ + β|1⟩ and γ|0⟩ + δ|1⟩ be two qubits’ states, then we can represent their system’s state as follows:
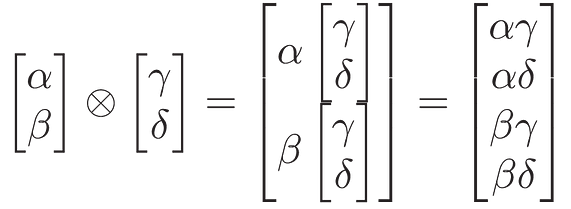
What every element of this column vector represents is the probability that the quantum system will collapse to a value of 0, 1, 2, or 3. In general, if we have n qubits we can represent a 2ⁿ-1 states. While we can always take the tensor product of 2 single-qubit states, not all two-qubit states can be denoted as a tensor product. In fact, such a system is said to be entangled.
Perhaps an even more intriguing phenomenon of quantum computing is entanglement. When two qubits are entangled, the quantum state of one qubit cannot be independently described of the state of the other. Whatever operations are performed upon one qubit also applies to the other qubit. In reality, entangled quantum particles maintain this property even if they are light years apart, which Einstein referred to as “spooky action at a distance”.
When one entangled qubit is measured, the other qubit’s superposition is also collapsed immediately. Hence, measuring the state of one qubit instantaneously provides information about the state of an entangled qubit, making this specific property incredibly useful.
All of these properties and phenomena are fascinating, but what can they be leveraged to do? What makes a quantum computer so revolutionary? There are some specific problems that only quantum computers can resolve. The most relevant, and arguably most notable, is that they break modern cryptography. In 1994, Peter Shor demonstrated that a quantum computer could break globally employed encryption algorithms like RSA. RSA underpins much of our digital world, being an integral part of web browsers, messenger apps, emails, VPNs, etc.
Additionally, quantum computers can be used for quantum simulations, allowing us to visualize and reproduce quantum interactions between molecules and atoms. This has massive ramifications in the fields of quantum chemistry and microbiology. They can improve the speed and performance of machine learning problems and can rapidly compute optimization algorithms no classical computer ever could.
For most users, using a quantum chip won’t make a noticeable difference when you’re browsing the web, texting a friend, or watching Netflix. But behind the scenes, quantum computing will wring in a new era of computation.
Quantum computing is forging the pathway for the future of computation, holding the potential to revolutionize everything from healthcare to finance. And you can be a part of that revolution.

